The nature of dark matter, the invisible substance that makes up over 80% of the matter in the universe, remains one of the most intriguing mysteries of modern physics. Elucidating the nature of dark matter will profoundly impact our understanding of cosmology, astrophysics, and particle physics, providing insights into the evolution of the Universe and potentially uncovering new physical laws and fundamental forces beyond the Standard Model.
Most efforts to directly detect dark matter have focused on Weakly Interacting Massive Particles (WIMPs) [1], but despite considerable efforts, there have been no conclusive signs of WIMP interactions with ordinary matter. This absence of WIMPs has attracted attention to ultralight (sub-eV) bosonic fields: another class of theoretically well-motivated dark matter candidates [2]. A wide variety of theories predict new spin-0 bosons such as axions and axion-like particles (ALPs) as well as spin-1 bosons such as dark and hidden photons [3].
Axions are particularly interesting, as they also provide a solution [4] to the so-called strong CP problem – a “fine-tuning” problem where quantum chromodynamics (QCD) does not nec- essarily conserve combined charge conjugation and parity inversion (CP) symmetry, but no CP violation has been observed in experiments – that is also compatible with the Sakharov conditions [5], where CP violation in the early universe is necessary to explain the current matter-antimatter imbalance.
Detection of such ultralight dark matter may be possible via interactions with standard model particles. Existing experiments involve detection of photons that would be created by the conversion of axions in strong electromagnetic fields via the inverse Primakoff effect [6–8] or dark-matter driven currents in electromagnetic systems [9]. More recently, another possibility has been proposed: dark-matter-driven spin-precession [10, 11].
The Cosmic Axion Spin Precession Experiment (CASPEr) is a multifaceted international research program using nuclear magnetic resonance (NMR) techniques to search for ultralight dark matter based on dark-matter-driven spin precession. CASPEr is naturally divided into two main research directions, based on two possible couplings to the Standard Model [11]:
- CASPEr-Wind searches for spin precession induced by the coupling between ALPs and the axial nuclear current. The interaction that drives the spin precession may be visualized as shown in Fig. 1A, where the nuclear spin couples to the relative momentum of the local ALP field.
- The coupling of axions to the gluon field, G, of quantum chromodynamics (QCD) is explored by CASPEr-Electric, which searches for the effect of an oscillating nuclear electric dipole moment (see Fig. 1B). In the presence of an electric field, this electric dipole moment generates a toque that drives spin precession.
For both CASPEr-Wind and CASPEr-Electric, this interaction can be treated as a pseudo- magnetic field BALP that drives nuclear spin precession, analogous to the behavior of a real magnetic field. The oscillation frequency of BALP is the Compton frequency, ωALP = mALPc2/ ħ, where mALP is the mass of the particle, c is the speed of light, and \hbar is the reduced Planck constant. The amplitude of BALP is related to a coupling parameter, gaNN for the CASPEr- Wind coupling or gd for the CASPEr-Electric coupling [11].
Based on this formulation, one can design an NMR experiment where BALP serves as the driving field, as shown schematically in Fig. 1C. A sample of polarized nuclear spins has its magnetization initially oriented by a leading field, B0, which is swept from B0,min to B0,max. If the Larmor frequency – defined as ωL = γIB0, where γI is the gyromagnetic ratio of the nucleus under investigation – is equal to the frequency of the driving field BALP, the nuclear spins will precess into the transverse plane. The resulting precessing magnetization generates a magnetic field that can be measured by a suitable detector, such as a superconducting quantum interference device (SQUID) [12], a tuned LC circuit, or an atomic magnetometer [13]. This signal transduction scheme is summarized in Fig. 1D, where it should be noted that the range of masses available to the search is determined by the range of achievable B0 values, as well as the nuclear gyromagnetic ratio. Furthermore, the sensitivity of the search to small coupling parameters is limited by the magnetic sensitivity of the detector, as well as the degree of polarization of the nuclear spins.
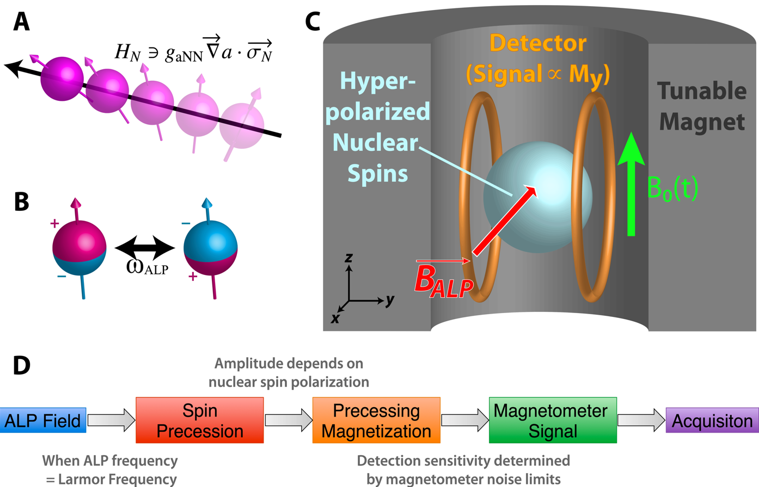
Figure 1: Overview of the Cosmic Axion Spin Precession Experiment (CASPEr). (A) The CASPEr-Wind coupling: nuclear spins precess about the relative local velocity of the dark matter field. (B) The CASPEr-E coupling: the QCD axion induces an oscillating nuclear electric dipole moment – in the presence of an electric field, this causes spin precession. (C) Schematic of the experimental configuration. A sample consisting of hyperpolarized nuclear spins is acted upon by the axion/ALP-induced effective magnetic field BALP. A tunable magnet produces a time-dependent field B0 such that when the nuclear Larmor frequency is equal to the dark matter Compton frequency, the nuclear spins will precess into the XY plane, resulting in measurable transverse magnetization. (D) The CASPEr signal transduction pathway, based on the use of polarized nuclear spins to convert the dark matter field into an observable magnetic field.
Preliminary CASPEr results have been obtained in the ultralight mass regime, utilizing existing zero- to ultralow-field (ZULF) NMR instrumentation [14, 15]. Experimental efforts to detect axion-like dark matter are underway for masses corresponding to the frequency range up to 4 MHz using a scannable superconducting magnet up to 0.1 T and a detection system based on superconducting quantum interference devices (SQUIDs). We refer to these ongoing low-frequency efforts as CASPEr-Wind-LF.
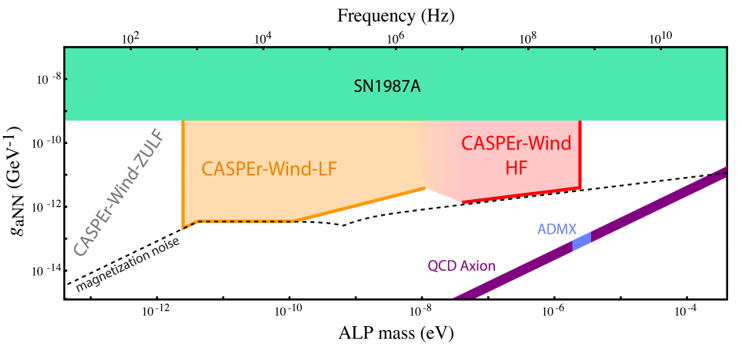
Figure 2: Projected reach of the first phase of CASPEr-Wind. Sensitivity of CASPEr-Wind-HF is expected to be limited by spin projection noise in the case of desired probe specifications.
Higher masses, corresponding to Compton frequencies of up to hundreds of MHz, are also of substantial interest. To explore this higher-frequency region of parameter space with CASPEr-Wind-HF (see Fig. 2), alternative equipment will be required. Using a spin-polarized nuclear target containing a high density of 1H nuclei and a superconducting magnet capable of reaching 14.1 T, it is possible to reach Larmor frequencies of 600 MHz, allowing overlap with other experiments, such as the Axion Dark Matter eXperiment (ADMX) [8]. However, measurement of nuclear spin precession at these frequencies requires different detectors from those used in CASPEr-Wind-LF. The most sensitive detectors than can reasonably operate across this wide range of frequencies are tunable LC circuits, cooled to cryogenic temperatures. We are currently developing suitable hyperpolarized samples and NMR detectors.

Martin Engler and Gary Centers checking that the components are precisely aligned while installing the CASPEr experiment at the University of Mainz. (Image: A. Wickenbrock / U. Mainz)
References:
[1] J. L. Feng, Annual Review of Astronomy and Astrophysics 48, 495 (2010).
[2] P. W. Graham, I. G. Irastorza, S. K. Lamoreaux, A. Lindner, and K. A. van Bibber, Annual Review of Nuclear and Particle Science 65, 485 (2015).
[3] L. Ackerman, M. R. Buckley, S. M. Carroll, and M. Kamionkowski, Phys. Rev. D 79, 023519 (2009).
[4] R. D. Peccei and H. R. Quinn, Phys. Rev. Lett. 38, 1440 (1977).
[5] A. D. Sakharov, Soviet Physics Uspekhi 34, 392 (1991).
[6] H. Primakoff, Phys. Rev. 81, 899 (1951).
[7] P. Sikivie, Phys. Rev. Lett. 51, 1415 (1983).
[8] N. Du, N. Force, R. Khatiwada, E. Lentz, R. Ottens, L. J. Rosenberg, G. Rybka, G. Carosi, N. Woollett, D. Bowring, et al. (ADMX Collaboration), Phys. Rev. Lett. 120, 151301 (2018).
[9] S. Chaudhuri, P. W. Graham, K. Irwin, J. Mardon, S. Rajendran, and Y. Zhao, Phys. Rev. D 92, 075012 (2015).
[10] D. Budker, P. W. Graham, M. Ledbetter, S. Rajendran, and A. O. Sushkov, Phys. Rev. X 4, 021030 (2014).
[11] P. W. Graham and S. Rajendran, Phys. Rev. D 88, 035023 (2013).
[12] J. Clarke and A. I. Braginski, The SQUID handbook: Applications of SQUIDs and SQUID systems (John Wiley & Sons, 2006).
[13] T. Wang, D. F. J. Kimball, A. O. Sushkov, D. Aybas, J. W. Blanchard, G. Centers, S. R. O. Kelley, A. Wickenbrock, J. Fang, and D. Budker, Physics of the Dark Universe 19, 27 (2018), ISSN 2212-6864.
[14] T. Wu, J. W. Blanchard, G. P. Centers, N. L. Figueroa, A. Garcon, P. W. Graham, D. F. J. Kimball, S. Rajendran, Y. V. Stadnik, A. O. Sushkov, et al., Phys. Rev. Lett. 122, 191302 (2019).
[15] A. Garcon, J. W. Blanchard, G. P. Centers, N. L. Figueroa, P. W. Graham, D. F. Jackson Kimball, S. Rajendran, A. O. Sushkov, Y. V. Stadnik, A. Wickenbrock, T. Wu, and D. Budker, Sci. Adv. 5 (2019).
Funder:

DFG, Reinhart Koselleck Projects
Project ID: 695405
Funded under: H2020-EU.1.1. – EXCELLENT SCIENCE – European Research Council (ERC)
