NV centers for eddy-currents imaging, ZULF magnetometry, and 3D magnetic field

Default

We use nitrogen-vacancy (NV) centers in diamond to produce pictures based on the magnetic fields created by eddy-currents [1]. Such an approach enables to discriminate different materials according to their conductivity. Our device has a bandwidth of 3.5 MHz and a spatial resolution of 0.3 mm.

From [1], the symbol of the city of Mainz. In the middle (b) – a photograph of the symbol. (a) and (c) are eddy-current imaging by NV of the phase (in a) and amplitude (in c) of the magnetic field from eddy current.

Then, we use NV centers as the magnetic field sensors at zero- and ultra-low magnetic field (ZULF) [2]. We refer to ZULF as the magnetic field’s range where the spin dynamics in a molecule is dominated by j-couplings (instead of the Zeeman effect). Then, Larmor frequency is much smaller than j-coupling frequency. NV centers are not used in ZULF often due to technical limitations which we overcome using frequency-modulated, circularly polarized microwaves. The use of such microwaves enables us to selectively drive resolved hyperfine transitions in NV centers.

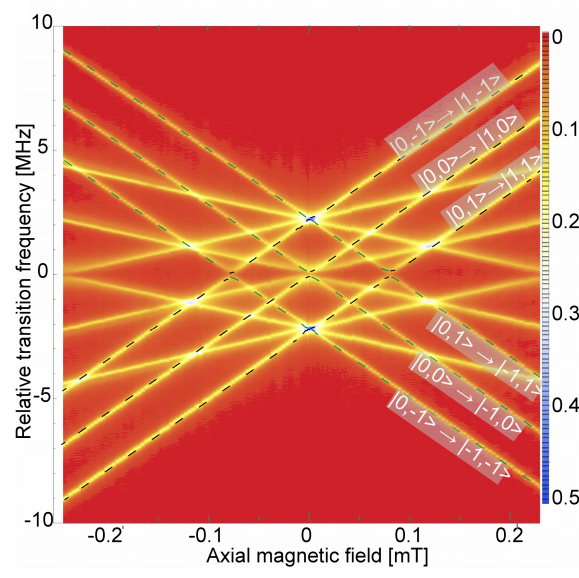
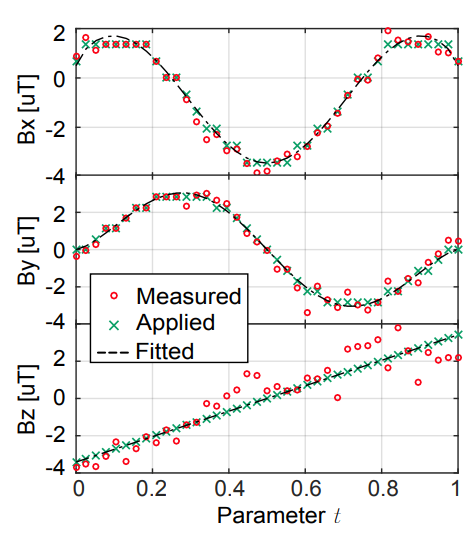
From [2], relative frequencies of transitions in NV centers as a function of the magnetic field acting on them. Labeled are the transitions matching NV centers, which are oriented along the direction of the applied magnetic field. The black dashed lines are the result of computer simulation.  The color scale indicates in percent the peak depth of the corresponding spectrum line, relative to the off-resonant case.

In a recent project, we took NV centers but, as opposed to [2], and similarly to [1], we did not use microwaves this time. Instead, we relied on ground state level anticrossing (GSLAC) in the triplet ground state (at 102.4 mT) to measure simultaneously all three spatial components of the magnetic field [3]. The benefit of GSLAC is that we have a sharp magnetic resonance (as a function of applied magnetic field) without microwaves. Thus, we obtained a 3D picture of the probed magnetic field!

From [3], measurements (in red) of the magnetic fields in three directions, as a function of the parameter describing the total applied (in green) magnetic field $ B =   \left\{ A cos(2 \pi t) , B sin (2 \pi t) , 6.82 t−3.41 \right\} $ where $ A = B = \sqrt{ R^2 – B z^2} $ .

References:

[1] Eddy-current imaging with nitrogen-vacancy centers in diamond, Georgios Chatzidrosos, Arne Wickenbrock, Lykourgos Bougas, Huijie Zheng, Oleg Tretiak, Yu Yang, and Dmitry Budker, Phys. Rev. Applied 11, 014060 (2019).   arXiv:1810.02723

[2] Zero-field magnetometry based on nitrogen-vacancy ensembles in diamond, Huijie Zheng, Jingyan Xu, Geoffrey Iwata, Till Lenz, Julia Michl, Boris Yavkin, Kazuo Nakamura, Hitoshi Sumiya, Takeshi Ohshima, Junichi Isoya, Joerg Wrachtrup, Arne Wickenbrock, Dmitry Budker, arXiv: 1811.11498 (2018).

[3] Microwave-free vector magnetometry with nitrogen-vacancy centers along a single axis in diamond, Huijie Zheng, Zhiyin Sun, Georgios Chatzidrosos, Chen Zhang, Kazuo Nakamura, Hitoshi Sumiya, Takeshi Ohshima, Junichi Isoya, Jörg Wrachtrup, Arne Wickenbrock, Dmitry Budker, arXiv:1904.04361 (2019).

Updated: December 12, 2022 — 1:27 pm